Mann-Whitney U-test
Posted on: April 9, 2010
- In: matematika | science
- 9 Comments
U-test ini digunakan untuk menguji signifikansi hipotesis komperatif dua sampel independen bila datanya berbentuk ordinal. Bila dalam suatu pengamatan data berbentuk interval, maka perlu dirubah dulu kedalam data ordinal. Bila masih berbentuk interval, sebenarnya dapat menggunakan t-test untuk pengujiannya, tetapi bila asumsi t-test tidak dipenuhi (misalnya data harus normal), maka t-test ini tidak dapat digunakan, atau dangan kata lain U-test digunakan sebagai alternatif lain dari t-test parametrik bila asumsi yang diperlukan bagi t-test tidak dipenuhi. U-test ini dapat menggunakan pengujian dua arah ataupun satu arah.
Bila besar sampel pertama dan kedua dinyatakan dengan n1 dan n2 (untuk n1 dan n2 yang lebih kecil dari 20), maka langkah pengujiannya adalah sebagai berikut:
- Gabungkan kedua sampel independen tersebut dan beri rangking pada tiap-tiap anggotanya. Dalam pemberian rangking kita asumsikan bahwa rangking 1 adalah untuk nilai yang paling rendah, rangking ke 2 untuk nilai yang lebih tinggi dan seterusnya hingga rangking yang paling tinggi. Apabila terdapat dua atau lebih nilai pengamatan yang sama, digunakan rangking rata-rata.
- Hitunglah jumlah rangking yang diperoleh pada masing-masing sampel, yaitu R1 untuk sampel
pertama dan R2 untuk sampel kedua.
-
Untuk uji statistik U, terdapat dua rumus yang digunakan, yaitu:

dan
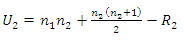
dimana :

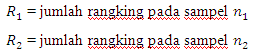
4. Dari dua nilai U tersebut yang digunakan adalah nilai U yang lebih kecil.
5. Bandingkan nilai U yang lebih kecil tersebut dengan nilai U tabel.

Contoh kasus (untuk n1 dan n1 yang lebih dari 20) :
Dilakukan penelitian untuk mengetahui adakah perbedaan kualitas manajemen antara Perguruan tinggi yang dianggap favorit oleh masyarakat dan Perguruan Tinggi yang tidak favorit. Penelitian menggunakan sampel 10 Perguruan Tinggi yang dianggap tidak favorit (A) dan 12 Perguruan Tinggi yang dianggap favorit (B). selanjutnya ke dua kelompok perguruan Tinggi tersebut di ukur kualitas manajemennya dengan menggunakan sebuah instrument, yang terdiri dari beberapa butir pertanyaan. Skor penilaian tertinggi 40 dan terendah 0. Data hasil penelitian adalah sebagai berikut :
A : 67 87 90 87 54 67 45 67 87 67
B : 78 90 98 79 67 89 90 89 79 98 78 89
Buktikan hipotesis yang menyatakan bahwa :
Perguruan Tinggi yang favorit dikelola dengan manajemen yang baik. (gunakan α = 0,025)
Jawab :
Berdasarkan hal tersebut di atas maka :
-
Judul penelitiannya dapat dirumuskan sebagai berikut :
Perbandingan kualitas manajemen Perguruan Tinggi yang Favorit dan Tidak Favorit
- Variable penelitiannya adalah :
- kualitas manajemen vatiabel independen
- favotitas Perguruan Tinggi variabel dependen
- Rumusan Masalah
adakah perbedaan kualitas manajemen yang signifikan antara Perguruan Tinggi yang favorit dan tidak favorit. - Sampel
terdiri dari dua kelompok Perguruan Tinggi yaitu Perguruan Tinggi tidak favorit (kelompok A) = 10 Perguruan Tinggi dan Perguruan Tinggi favorit (kelompok B) = 12 Perguruan Tinggi. - Hipotesis :

-
Penyajian data :
| Kel. A |
Nilai kualitas |
Rangking |
Kel. B |
Nilai kualitas |
Rangking |
| 1 |
67 |
5 |
1 |
78 |
8,5 |
| 2 |
87 |
13 |
2 |
90 |
19 |
| 3 |
90 |
19 |
3 |
98 |
21,5 |
| 4 |
87 |
13 |
4 |
79 |
10,5 |
| 5 |
54 |
2 |
5 |
67 |
5 |
| 6 |
67 |
5 |
6 |
89 |
16 |
| 7 |
45 |
1 |
7 |
90 |
19 |
| 8 |
67 |
5 |
7 |
89 |
16 |
| 9 |
87 |
13 |
9 |
79 |
10,5 |
| 10 |
67 |
5 |
10 |
98 |
21,5 |
| 11 |
11 |
78 |
8,5 |
||
| 12 |
12 |
89 |
16 |
||
|
R1= 81 |
R2= 172 |
-
Perhitungan :
Dari tabel di atas diperoleh R1 = 81 dan R2= 172. Nilai U diperoleh dengan perhitungan :
Ternyata nilai U2 lebih kecil dari U1 dengan demikian nilai U yang digunakan untuk membandingkan dengan U tabel adalah U2. Berdasarkan tabel dengan α = 0,025 (satu arah) atau α = 0,05 (dua arah) dengan n1 = 10 dan n2 = 12 diperoleh nilai Uα (U tabel) = 29. Ternyata nilai U hitung lebih kecil dari pada U tabel (26 < 29), dengan demikian H0 ditolak.
8. Kesimpulan :
Terdapat perbedaan kualitas manajemen yang signifikan antara perguruan tinggi yang favorit dan tidak favorit. Berarti Perguruan Tinggi yang favorit dikelola dengan manajemen yang baik.
9. Saran :
Perguruan tinggi yang tidak favorit perlu meningkatkan kualitas manajemennya bila ingin menjadi perguruan tinggi yang favorit.
Bila n1 atau n2 atau kedua-duanya sama atau lebih besar dari 20, digunakan pendekatan kurva normal (mendekati distribusi normal), dengan :


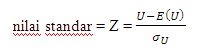
Angka sama (Ties). Mann-whitney U-test menganggap bahwa nilai-nilai itu memiliki suatu distribusi yang kontinyu. Dengan pengukuran yang sangat tepat pada variable yang kontinyu, kemungkinan terjadinya angka yang sama adalah nol. Tetapi, dengan ukuran-ukuran yang relative kasar, yang biasa kita pergunakan dalam penelitian ilmiah mengenai perilaku, angka sama sangat mungkin terjadi. Kita anggap bahwa dua observasi yang menghasilkan angka sama sungguh-sungguh berbeda, tetapi bahwa perbedaan itu terlalu halus atau kecil sehingga tidak terlacak oleh pengukuran kita yang kasar itu.
Bila angka sama terjadi, kita berikan kapada masing-masing observasi (nilai) itu rata-rata rangking yang akan mereka miliki seandainya angka sama itu tidak terjadi.
Jika angka sama antara dua observasi atau lebih dalam kelompok yang sama, harga/nilai U tidak terpengaruh. Tetapi jika angka sama itu muncul antara dua observasi atau lebih dan menyangkut kedua kelompok, harga/nilai U terpengaruh. Sungguhpun akibat itu biasanya dapat diabaikan, suatu koreksi untuk angka sama tersedia untuk dipergunakan dengan pendekatan kurva normal yang kita pergunakan untuk sampel-sampel besar.
Akibat dari rangking-rangking yang sama adalah mengubah variabilitas himpunan rangking itu. Dengan demikian, koreksi untuk angka sama harus diterapkan pada standar deviasi distribusi sampling U. setelah dikoreksi untuk angka sama, standar deviasi itu menjadi :



∑T diperoleh dengan menjumlahkan harga-harga T semua kelompok yang memiliki observasi-observasi berangka sama. Dengan koreksi untuk angka sama ini, kita dapatkan Z dengan :


Contoh kasus (untuk n1 atau n2 atau kedua-duanya sama atau lebih besar dari 20)
Ujian matematika diberikan kepada sebanyak 20 orang mahasiswa Universitas Terbuka yang dipilih secara random untuk wilayah DKI dan ujian yang sama pula diberikan kepada 15 orang mahasiswa Universitas Terbuka yang dipilih secara random di wilayah Ujungpandang (Sulsel). Dari hasil ujian yang diperoleh di dua tempat (daerah) diatas DKI dan sulsel menunjukkan nilai ujian tiap mahasiswanya sebagai berikut :
| No |
DKI (grup A) |
Sulsel (grup B) |
| 1 |
70 |
72 |
| 2 |
63 |
67 |
| 3 |
78 |
56 |
| 4 |
71 |
69 |
| 5 |
82 |
71 |
| 6 |
93 |
59 |
| 7 |
96 |
55 |
| 8 |
61 |
88 |
| 9 |
72 |
79 |
| 10 |
63 |
49 |
| 11 |
56 |
76 |
| 12 |
82 |
53 |
| 13 |
66 |
66 |
| 14 |
76 |
73 |
| 15 |
67 |
80 |
| 16 |
61 |
|
| 17 |
74 |
|
| 18 |
86 |
|
| 19 |
64 |
|
| 20 |
93 |
|
| 21 |
97 |
Pengujian tersebut dilakukan untuk mengetahui apakah ada perbedaan penampilan (tingkat kepandaian) mahasiswa Universitas Terbuka pada kedua wilayah diatas. (tingkat= 5% (pengujian dengan dua arah)).
Jawab :
-
Judul penelitiannya dapat dirumuskan sebagai berikut :
Perbandingan penampilan (tingkat kepandaian) mahasiswa Universitas Terbuka di wilayah DKI dan ujungpandang (Sulsel).
- Variabel penelitiannya adalah :
- Hasil ujian variabel independen
- Tingkat kepandaian mahasiswa variabel dependen
- Rumusan masalah :
Adakah perbedaan tingkat kepandaian yang signifikan antara Universitas Terbuka di wilayah DKI dan sulsel. - Sampel
Terdiri dari 21 orang mahasiswa universitas terbuka untuk wilayah DKI dan 15 orang mahasiswa universitas terbuka untuk wilayah ujungpandang (Sulsel). - Hipotesis
H0: Tidak ada perbedaan tingkat kepandaian yang signifikan antara mahasiswa universitas terbuka di wilayah DKI dan mahasiswa universitas terbuka di wilayah Sulsel.H1: Ada perbedaan tingkat kepandaian yang signifikan antara mahasiswa universitas terbuka di wilayah DKI dan mahasiswa universitas tebuka di wilayah Sulsel. - Penyajian data :
Tabel nilai hasil ujian beserta rangkingnya
| No |
Grup A |
Rangking |
Grup B |
Rangking |
| 1 |
70 |
17 |
72 |
20,5 |
| 2 |
63 |
9,5 |
67 |
14,5 |
| 3 |
78 |
26 |
56 |
4,5 |
| 4 |
71 |
18,5 |
69 |
16 |
| 5 |
82 |
29,5 |
71 |
18,5 |
| 6 |
93 |
33,5 |
59 |
6 |
| 7 |
96 |
35 |
55 |
3 |
| 8 |
61 |
7,5 |
88 |
32 |
| 9 |
72 |
20,5 |
79 |
27 |
| 10 |
63 |
9,5 |
49 |
1 |
| 11 |
56 |
4,5 |
76 |
24,5 |
| 12 |
82 |
29,5 |
53 |
2 |
| 13 |
66 |
12,5 |
66 |
12,5 |
| 14 |
76 |
24,5 |
73 |
22 |
| 15 |
67 |
14,5 |
80 |
28 |
| 16 |
61 |
7,5 |
||
| 17 |
74 |
23 |
||
| 18 |
86 |
31 |
||
| 19 |
64 |
11 |
||
| 20 |
93 |
33,5 |
||
| 21 |
97 |
36 |
||
|
|
R2 = 232 |
7. Perhitungan :
Dari tabel di atas diperoleh R1 = 434 dan R1 = 232. Nilai U diperoleh dengan perhitungan:

Dari dua nilai U tersebut, ternyata nilai U1 lebih kecil dari nilai U2, dengan demikian nilai U yang digunakan dalam perhitungan selanjutnya adalah U1.
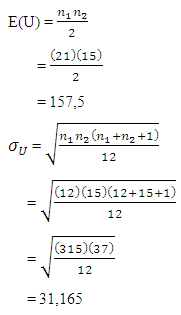

8. Kesimpulan
Ada perbedaan tingkat kepandaian yang signifikan antara mahasiswa universitas terbuka di wilayah DKI dan mahasiswa universitas terbuka di wilayah Sulsel.
9. Saran
Universitas terbuka tersebut perlu meningkatkan kualitas manajemennya.
Karena dalam data di atas terdapat observasi yang berangka sama (nilai yang sama) , maka kita coba lakukan koreksi untuk angka sama. Untuk data itu, diperoleh :
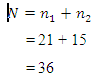
Kita lihat kelompok-kelompok yang berangka sama sebagai berikut :
2 nilai 56
2 nilai 61
2 nilai 63
2 nilai 66
2 nilai 67
2 nilai 71
2 nilai 72
2 nilai 76
2 nilai 82
2 nilai 93
Jadi kita punya harga t sebesar 2.

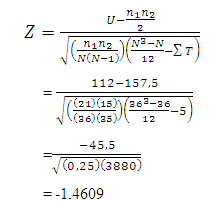
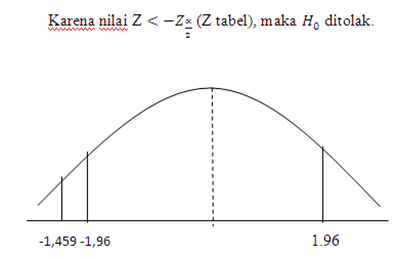
Nilai Z dengan koreksi untuk angka sama adalah sedikit lebih besar daripada yang ditemukan sebelummya jika koreksi tidak dijalankan. Dari contoh kasus tersebut, akibat angka sama hanya kecil saja.
9 Tanggapan to "Mann-Whitney U-test"
kak irun,,,
hehe…mksih wat infox kk,,
kget td wkt tak buka liat blogx kk,,
alhmdulilah ada tmbhan wat analisis data hsil pnlitian kak.
keknya ada yg keliru deh mbak.
“Ternyata nilai U hitung lebih kecil dari pada U tabel (26 < 29), dengan demikian ditolak." yg contoh kasus pertama
Good job. Thanks
mencari t hitung bagaimana kaka ?
Mb…untuk contoh kasus yg jumlah sampelnya besar, sepertina Ho diterima the…karena harga atau nila Z lebih kecil dari Z tabel….Coba lihat lagi kriteria pengambilan keputusan, lalu bandingkan dengan harga Z = – 1, 45997. Konfirmasi ya? Thanks.
mb, saya lihat beberapa contoh nilai Z tabel selalu 1,96 termasuk punya mbak. itu memang sudah ketentuan atau ada cara mencarinya? kalau memang ada caranya mohon di share ya, Terima Kasih 🙂
mbak mau tanya kalau mencar z tabel untuk n1=36 dan n2=36 gimana caranya mbak??
mohon bantuannya mbak
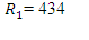



Juni 6, 2010 pada 2:10 am
makasih ya cantik infonya… lumayan tambahan buat belajar 🙂
Juni 6, 2010 pada 9:14 am
sama-sama…. 🙂 🙂